Алгоритмы автопилота посадки роботизированного дирижабля
Аннотация
В работе рассмотрены алгоритмы функционирования автопилота робота-дирижабля в режиме посадки. Рассмотрены базовые алгоритмы управления дирижаблей. Предложен новый способ формирования требований к траектории дирижабля в режиме посадки, обеспечивающий компенсацию бокового ветра без применения подруливающих даигателей и карданной схемы размещения движителей. Представленные результаты могут быть использованы при проектировании автопилотов роботизированных воздухоплавательных платформ.
Ключевые слова: автопилот, управление, посадка, дирижабль, робот
Современный уровень развития воздухоплавания заново открывает перспективы применения дирижаблей для решения задач транспортировки, мониторинга и наблюдения [1]. При решении любой задачи система управления дирижаблем должна обеспечивать возможность безопасного взлета и посадки в широком диапазоне метеоусловий. Режимы взлета и посадки являются наиболее аварийными и сложными при управлении дирижаблем в силу ограниченности органов управления в этих режимах, существенным изменением аэродинамических характеристик дирижабля при движении вблизи поверхности, сильным влиянием ветровых возмущений. В этой связи актуальной ставиться задача автоматического взлета и посадки с обеспечением требуемых уровней безопасности и показателей качества системы управления дирижабля как роботизированного средства.
Постановка задачи
Задача автопилота посадки состоит в реализации следующих этапов:
- выбор направления (траектории) посадки;
- движение к точке посадки;
- причаливание.
Посадка современных дирижаблей осуществляется, как правило, к причальной мачте. В условиях малых ветровых воздействий возможны как посадка по наклонной траектории, так и вертикальная посадка.
При посадке в условиях ветра возможны следующие варианты постановки задачи:
- причальная мачта допускает подход дирижабля с любого направления. В этом случае оптимальным с точки зрения минимизации действия ветровых возмущений является выбор направления захода на посадку против ветра;
- посадка в условиях бокового ветра. В этом случае для компенсации сноса используют технику упреждения по курсу – поворот носа дирижабля против ветра.
Для обеспечения навигации на этапе движения к точке посадки используется интегрированная (инерциальная и спутниковая) навигационная система. Дополнительно для измерения расстояния до поверхности используется лазерный дальномер.
На этапе причаливания для повышения точности относительного позиционирования дирижабля и причальной мачты могут использоваться визуальные методы навигации.
В данной работе предлагаются структура и алгоритмы автопилота посадки для управления движением дирижабля к точке посадки. Способы взаимодействия с причальной мачтой (сброс и соединение тросов) зависят от конкретной реализации дирижабля и причальных устройств и в данной статье не рассматриваются.
Органы управления дирижабля
Будем рассматривать наиболее распространенную в современных дирижаблях схему расположения органов управления с измененяемым вектором тяги движителей. Эта схема (рис. 1) предполагает наличие двух винтов, которые можно поворачивать независимо друг от друга в вертикальной плоскости (такую схему также называют пилонной) и регулировать тяги. Таким образом, каналами управления в данной схеме являются [2]:
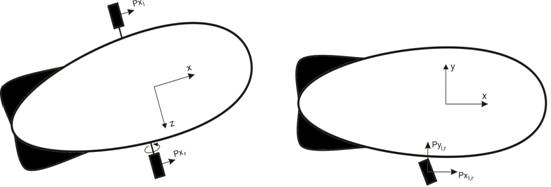
Рис. 1. Силы и моменты в схеме с двумя движителями
- тяги левого и правого движителей;
- углы поворота левого и правого движителя в вертикальной плоскости.
Пилонная схема формирует силы, действующие вдоль вертикальной и продольной осей, и моменты относительно этих осей. В этой связи дирижабль должен быть сбалансирован по углам тангажа и крена. Такая схема не позволяет непосредственно компенсировать боковые возмущения (например, боковые порывы ветра). Так как отсутствует управляющая боковая сила, требуется применение соответствующих алгоритмов для изменения ориентации дирижабля в соответствии с целью движения и возмущающими воздействиями.
При достаточной воздушной скорости могут быть задействованы аэродинамические рули, создающие дополнительные управляющие моменты. При использовании пилонной схемы целесообразно также применять менее мощные рулевые двигатели, которые используются только в режимах причаливания и отчаливания.
При наличии баллонетов они могут быть использованы для управления подъемной силой и моментом по тангажу.
Алгоритмы движения к точке посадки
Будем рассматривать математическую модель дирижабля, основанную на модели движения твердого тела, в виде [2]:![]() (1)
(1)![]() (2)
(2) , (3)
, (3)
где х – вектор скоростей дирижабля в базовой системе координат; М – матрица массо-инерционных параметров; ![]() – вектор управляющих сил и моментов, здесь l – вектор конструктивных параметров;
– вектор управляющих сил и моментов, здесь l – вектор конструктивных параметров; ![]() – вектор нелинейных элементов динамики дирижабля;
– вектор нелинейных элементов динамики дирижабля; ![]() – вектор измеряемых и неизмеряемых внешних возмущений; δ – вектор управляемых координат; K – матрица коэффициентов управления; U – вектор управляющих воздействий;
– вектор измеряемых и неизмеряемых внешних возмущений; δ – вектор управляемых координат; K – матрица коэффициентов управления; U – вектор управляющих воздействий; ![]() – вектор положения P и ориентации
– вектор положения P и ориентации ![]() (выходных координат) связанной системы координат относительно базовой;
(выходных координат) связанной системы координат относительно базовой; ![]() – вектор кинематических связей;
– вектор кинематических связей; ![]() – вектор линейных скоростей связанной системы координат относительно базовой;
– вектор линейных скоростей связанной системы координат относительно базовой; ![]() – вектор угловых скоростей связанной системы координат относительно базовой.
– вектор угловых скоростей связанной системы координат относительно базовой.
Обобщенные методы конструирования систем управления дирижаблями рассмотрены в [2 – 6]. Наибольшее распространение получили классические для летательных аппаратов подходы, предполагающие разделение движения на продольную и поперечную составляющие с дальнейшей линеаризацией модели. Линейное управление обеспечивает устойчивость в небольшой окрестности равновесного состояния, относительно которого выполнена линеаризация.
В силу того, что математическая модель дирижабля (1) – (3) представляет собой многосвязную систему нелинейных дифференциальных уравнений, наибольший интерес представляют нелинейные методы конструирования систем управления. В нелинейной постановке широкое распространение получили методы синтеза систем управления на основе обратных задач динамики.
В работах [2, 5] предложены процедуры синтеза нелинейных систем управления дирижаблей, позволяющих решать позиционные и траекторные задачи. Желаемые требования к траектории в пространстве Rn внешних координат задаются выражением [2]: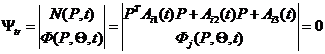 ,
,![]() ,
,![]() , (4)
, (4)![]() ,
, ![]()
где Aij – матрицы коэффициентов соответствующей размерности, определяющих траекторию; ![]() – размерность пространства функционирования дирижабля; μ– размерность вектора
– размерность пространства функционирования дирижабля; μ– размерность вектора ![]() , задающего требования к углам ориентации дирижабля; ξ – параметр, принимающий значение 0 (для позиционной задачи) или 1 (для случая движения с заданной скоростью).
, задающего требования к углам ориентации дирижабля; ξ – параметр, принимающий значение 0 (для позиционной задачи) или 1 (для случая движения с заданной скоростью).
Алгоритм позиционно-траекторного управления имеет вид [2]:![]() , (5)
, (5)
где ![]() – оценка вектора внешних сил и моментов,
– оценка вектора внешних сил и моментов, ![]() – диагональные матрицы задаваемых настроек, определяющих характер переходного процесса, выражения матриц K0, K1, K2, представлены в [2].
– диагональные матрицы задаваемых настроек, определяющих характер переходного процесса, выражения матриц K0, K1, K2, представлены в [2].
В данном алгоритме желаемые углы ориентации дирижабля ![]() в (4) предлагалось задавать извне планировщиком [2]. При этом предполагается возможность реализации боковой управляющей силы. Однако на малых угловых скоростях при отсутствии боковой управляющей силы планировщик должен согласовывать требования к траектории и ориентации. Например, можно задавать желаемый угол по касательной к траектории. Но при этом не вполне учитываются свойства модели дирижабля. Так, для компенсации возникшей боковой скорости или бокового возмущения дирижабль должен повернуться по курсу по направлению, отличному от касательного к траектории (техника с упреждением по курсу).
в (4) предлагалось задавать извне планировщиком [2]. При этом предполагается возможность реализации боковой управляющей силы. Однако на малых угловых скоростях при отсутствии боковой управляющей силы планировщик должен согласовывать требования к траектории и ориентации. Например, можно задавать желаемый угол по касательной к траектории. Но при этом не вполне учитываются свойства модели дирижабля. Так, для компенсации возникшей боковой скорости или бокового возмущения дирижабль должен повернуться по курсу по направлению, отличному от касательного к траектории (техника с упреждением по курсу).
В условиях изложенных выше особенностей представляется целесообразным задавать только желаемую траекторию или позицию без предъявления требований к углам ориентации (![]() = 0). В этом случае ориентация дирижабля должна выбираться регулятором на основе многосвязной нелинейной модели.
= 0). В этом случае ориентация дирижабля должна выбираться регулятором на основе многосвязной нелинейной модели.
Для этой цели предлагается задавать желаемое движение некоторой точки дирижабля, смещенной относительно центра масс на расстояние xu в продольном направлении. Для этой точки возможно управление в поперечном направлении за счет поворота дирижабля по курсу. Матрица массо-инерционных параметров в (5) будет иметь вид:
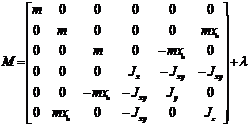 ,
,
где m – масса дирижабля, Jx, Jy, Jz, Jxy – моменты инерции, ![]() – матрица присоединенных масс. Элементы
– матрица присоединенных масс. Элементы ![]() в M являются следствием применения формулы Эйлера для связи ускорений точек твердого тела и связывают продольное и вращательное движение.
в M являются следствием применения формулы Эйлера для связи ускорений точек твердого тела и связывают продольное и вращательное движение.
Оценка внешних сил и моментов
Оценка внешних сил и моментов ![]() производится при помощи аналитического выражения известных сил тяжести, Архимеда, аэродинамической силы (на основе полученных в результате программной продувки аэродинамических коэффициентов) и их моментов, а также с использованием наблюдателя неизмеряемых внешних возмущений.
производится при помощи аналитического выражения известных сил тяжести, Архимеда, аэродинамической силы (на основе полученных в результате программной продувки аэродинамических коэффициентов) и их моментов, а также с использованием наблюдателя неизмеряемых внешних возмущений.
При наличии на борту дирижабля датчика ветра возможно оценивание воздушной скорости дирижабля на основе его показаний. Тогда в выражения для аэродинамических сил подставляются не скорости дирижабля, полученные навигационной системой, а воздушные скорости.
Следует отметить, что даже с применением датчика ветра невозможно оценить все внешние возмущения (т.к. датчик дает данные о воздушной скорости только в области его установки – как правило, на носу, оценки аэродинамических коэффициентов и других параметров дирижабля не точны). Поэтому в структуру автопилота необходимо включить наблюдатель. В работах [2, 6, 7] рассмотрены подходы к построения наблюдателей. Уравнение нелинейного наблюдателя возмущений Луенбергера имеет вид:
![]() ,
,![]() ,
,
где L – диагональная матрица с постоянными положительными коэффициентами, обеспечивающая асимптотическую устойчивость процесса оценивания, F – аналитическая оценка внешних сил, ![]() – оценка неизмеряемых внешних сил,
– оценка неизмеряемых внешних сил, ![]() – вспомогательная переменная.
– вспомогательная переменная.
Полученные оценки неизмеряемых внешних сил ![]() используются для формирования вектора
используются для формирования вектора ![]() и передаются в регулятор. Разделение регулятора и наблюдателя допустимо при высоком быстродействии процессов оценивания [2].
и передаются в регулятор. Разделение регулятора и наблюдателя допустимо при высоком быстродействии процессов оценивания [2].
Результаты моделирования алгоритмов автопилота для движения к точке посадки
На рисунках 2 – 6 представлены результаты моделирования автопилота посадки роботизированного дирижабля. Дирижабль начинает движение из точки (25, 50, 35) м с начальной скоростью Vx = 5 м/с. Задана точка посадки (цель позиционного управления) в начале координат. Моделирование останавливается при расстоянии от дирижабля до точки посадки менее 3 м.
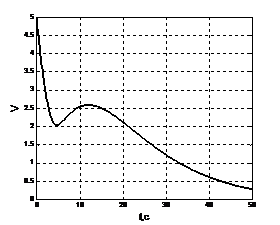
На рисунках 2, 3, 4 показаны траектория, скорость и ориентация по курсу дирижабля при движении без внешних возмущений.
 Рис. 2. Траектория дирижабля при движении без внешних возмущений |
|

Рис. 4. Ориентация дирижабля на траеткории при движении без внешних возмущений
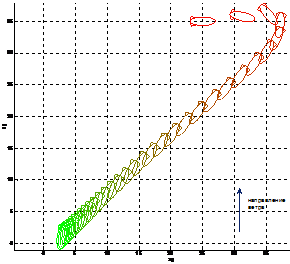
На рисунке 5 показана ориентация дирижабля на траектории при воздействии ветра параллельно оси x базовой системы координат, на рисунке 6 – параллельно оси z. Символическое изображение дирижабля построено через равные промежутки времени, т.е. чем чаще эти изображения, тем меньше скорость на данном участке траектории.
 Рис. 5. Ориентация дирижабля на траеткории при ветре вдоль оси x |
|
Представленные результаты моделирования показывают эффективность использованных адгоритмов автопилота движения к точке посадки, в том числе в услових ветровых возмущений. Алгоритм автоматически реализует управление ориентацией дирижабля для противодействия ветру.
Заключение
В статье рассмотрены алгоритмы функционирования автопилота робота-дирижабля в режиме посадки. Рассмотрены базовые алгоритмы управления дирижаблей. Предложен новый способ формирования требований к траектории дирижабля в режиме посадки, обеспечивающий компенсацию бокового ветра без применения подруливающих даигателей и карданной схемы размещения движителей. Представленные результаты могут быть использованы при проектировании автопилотов роботизированных воздухоплавательных платформ.
Литература
- 1.Верба Г.Е., Голубятников В.Н., Кирилин A.Н., Пшихопов B.X., Старостин И.А., Ступников В.И. Современное состояние и перспективы использования воздухоплавательных комплексов // Мехатроника, автоматизация, управление. – 2009. № 3. С. 40-42.
2.Пшихопов В.Х., Медведев М.Ю., Федоренко Р.В., Сиротенко М.Ю., Костюков В.А., Гуренко Б.В. Управление воздухоплавательными комплексами: теория и технологии проектирования. – М.: ФИЗМАТЛИТ, 2010. – 394 с.
3.Moutinho A.B. Modeling and nonlinear control for airship autonomous flight. Ph.D. thesis, Instituto Superior Tecnico, Technical University of Lisbon., 2007.
4.Emmanuel Hygounenc, Il-Kyun Jung, Philippe Soures, and Simon Lacroix. The autonomous blimp project of LAAS-CNRS: Achievements in flight control and terrain mapping. The International Journal of Robotics Research, 23(4-5):473–511, 2004.
5.Пшихопов В.Х., Медведев М.Ю., Сиротенко М.Ю., Носко О.Э., Юрченко А.С. Проектирование систем управления роботизированных воздухоплавательных комплексов на базе дирижаблей // Известия ТРТУ. Тематический выпуск «Перспективные системы и задачи управления». – Таганрог, – 2006. – № 3 (58). – С. 160–167.
6.Пшихопов В.Х., Медведев М.Ю. Структурный синтез автопилотов подвижных объектов с оцениванием возмущений // – М.: Информационно-измерительные и управляющие системы. – 2006. – №1. – С.103–109.
7.Пшихопов В.Х., Медведев М.Ю. Синтез адаптивных систем управления летательными аппаратами // Известия Южного федерального университета. Технические науки. – 2010. – Т. 104. – № 3. – С. 187-196.