Сходимость метода теоретического моделирования спектров рентгеновского поглощения XANES за Ru L_2,3-краями в рамках теории функционала плотности  (DFT) на примере кристаллов [Ru(NH₃)₆]³⁺

Аннотация

И.Г. Альперович

Представлены результаты анализа вычислительных аспектов метода получения спектров XANES за Ru L2,3-краями с помощью интегрирования дипольных матричных элементов перехода с привлечением DFT. Показана сходимость численной процедуры интегрирования для параметров, использованных в ранее опубликованных работах, на примере кристаллов [Ru(NH3)6]3+. Конкретней, доказывается, что можно использовать малую область интегрирования и достаточно большой шаг между точками, что позволяет минимизировать требования к вычислительным мощностям и открывает перспективы использования этого метода для моделирования спектров XANES в рутений–координированных катализаторах расщепления воды для исследований в области солнечной энергетики.
Ключевые слова: RuLedge, XANES, DFT, теория функционала плотности, рентгеновская спектроскопия поглощения,   гексоаминорутений, Ru(NH3)6.

Ключевые слова:

01.04.07 - Физика конденсированного состояния

Введение.

Одним из эффективных и стремительно развивающихся методов исследования веществ в физике твердого тела является рентгеновская спектроскопия поглощения в ближней области (XANES - X-ray absorption near edge structure) [1]. Будучи комплементарной к методике анализа кристаллической структуры EXAFS, она позволяет в т.ч. определять углы между атомами и окислительное состояние исследуемых материалов [2]. Несмотря на недавние успехи, связанные с появлением  новых источников синхротронного излучения и развитием теории, эта техника до сих пор не имеет математического аппарата, который позволил бы вычислять спектры XANES в рамках единого подхода. Это приводит к тому, что иногда спектры некоторых веществ, например содержащих элементы переходного ряда, нельзя удовлетворительно описать теоретически [3] общепринятыми методами. Спектры XANES за Ru L_2,3-краями – как раз один из таких случаев [4]. Для успешного теоретического моделирования указанных спектров рентгеновского поглощения в рутений-содержащих веществах (кристаллах гексоаминорутения [Ru(NH₃)₆]³⁺ и представляющих интерес для искусственного фотосинтеза катализаторов расщепления воды [5]), была разработана методика, базирующаяся на релятивистской теории функционала плотности (DFT) [6]. Она отлично зарекомендовала себя для решения поставленной задачи (подробности метода приведены в работе [7]), отличаясь в т.ч. высокой эффективностью в плане затрат «время-вычислительные ресурсы». Это было достигнуто за счет того, что область и шаг численного интегрирования дипольных матричных элементов в ходе теоретических расчетов выбирались особым образом. В представленной работе приводятся детали и соображения, на основе которых эти параметры выбирались.

Результаты и обсуждение.

Поскольку метод основан на численном интегрировании матричных элементов перехода с Ru 2p-орбиталей на свободные состояния (LUMO) в соответствии с «золотым правилом Ферми» (1),
то получаемые спектры зависят от двух параметров: области и шага интегрирования. Обе величины определяют число точек N по которым ведется интеграция, а значит и скорость вычислений (~N3). Они должны выбираться так, чтобы разница между расчетным и истинным интегралами (с бесконечными пределами) была пренебрежимой. Рассмотрим влияние обоих параметров на примере Ru L_2,3 XANES спектров кристалла [Ru(NH₃)₆]³⁺.
Оценка трехмерной области интеграции вокруг атома Ru. Рассмотрим область трехмерной интеграции вокруг атома Ru в (1): ненулевой вклад в интегралы (1) следует ожидать от пространственной области, где обе волновые функции Y отличны от нуля. Таким образом, можно ограничить бесконечные пределы интегрирования до области, содержащей бОльшую часть электронной плотности орбиталей Ru Ψ_2p, скажем 99% (значение, взятое за infinum – нижнюю границу – при анализе). Поскольку орбитали рутения Ψ_2p, которые покидает фотоэлектрон при поглощении рентгеновского кванта в эксперименте по записи спектров XANES, геометрически расположены близко к ядру Ru, то их можно охарактеризовать как высоко-локализованные и на практике проводить численное интегрирование для выбранной области за небольшое время (порядка нескольких часов) даже используя обычные вычислительные мощности.
Рассмотрим подробней, почему достаточное значение ребра кубической сетки вокруг поглотителя-рутения можно взять (и это будет значением "с большим запасом") равным 0.45 Å как в работе [7]. Первая, чисто теоретическая оценка области, содержащей 99% электронной плотности 2p-уровней атома(ов) рутения была сделана в результате анализа решения уравнения Шредингера для водородоподобных атомов. Уравнение (2) описывает вероятность W(→r) нахождения электрона с волновой функцией Ψ_Hydrogen в единице объема d→r - т.е. плотность распределения. Интеграция (2) по телесному углу dΩ дает вероятность нахождения электрона в сферическом слое толщиной dr(3):

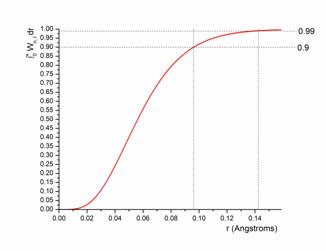
Искомая вероятность локализации 2р-электронов рутения в любом месте сферы радиусом r с центром в "месте нахождения" поглотителя Ru получается путем подстановки n=2, l=1, Z=44 (т.е. значений для Ru 2p-электронов) и интегрированию (3) по радиусу r используя радиальные функции R_n,_l (Рис. 1). Видно, что для этой, безусловно упрощенной модели, более 99% от электронной плотности локализовано в пределах 0.15 Å от атома Ru.

Рисунок 1. Оценка интегральной вероятности локализации 2р-электронов на расстоянии r от поглотителя-Ru при использовании модели водородоподобного атома. Отмечены точки, соответствующие ординатам в 90% и 99%.

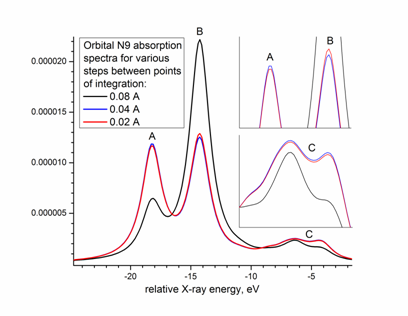
Рисунок 2. Пример рентгеновского спектра поглощения, вычисленного в подходе из [7] в результате расчетов возбуждений 9-й остовной орбитали рутения в спектрах XANES [Ru(NH3)6]3+ за Ru L3-краем. Показаны результаты при различных значениях "шага интегрирования по трехмерной сетке", соответствующих расстоянию между точками числовой сетки интеграции. Черная, синяя и красная кривые соответствуют расстояниям между точками в 0.08 Å, 0.04 Å и 0.02 Å, соответственно, вставки содержат увеличенные области графика.

Для сравнения, функция радиального распределения 2р-электронной плотности в изолированном атоме Ru была также получена численно, с помощью свободно-распространяемой программы “Energy” (http://grants.rsu.ru/osi/atom/index-e.html). Эта программа осуществляет самосогласованное решение уравнения Шредингера в приближении Хартри-Фока для электронов конкретной оболочки с заданным модулем орбитального момента в выбранном атоме. Вычисленное распределение находится в хорошем согласии с аналитической оценкой и подтверждает, что 2р-волновая функции локализованы в пределах сферы радиуса ~ 0.15 Å. Эти предварительные выводы об области локализации подынтегральных функций подтверждаются и другими способами.
Так, еще один косвенный способ оценки локализации 2p-волновых функций рутения - построение эквипотенциальной поверхности |Ψ_2p| в трехмерном пространстве с помощью DFT-программы ADF2010. Соответствующие изображения молекулярных орбиталей (здесь не приведены) находятся в согласии с другими оценками, что подтверждает адекватность выбранной области интегрирования задаче минимизации временных затрат на вычисления. Наконец, следует отметить, что спектры XANES, рассчитанные для разных размеров области интегрирования (при одинаковом шаге, здесь не приведены) действительно показывают сходимость уже до радиуса в 0.45 Å.
Оценка шага интегрирования матричных элементов (2). На Рис. 2 показаны результаты вычисления (1) для вещества [Ru(NH₃)₆]³⁺ с разным шагом между точками трехмерной сетки интегрирования в пределах между 0.02-0.08 Å, где 0.04 Å оказалось уже достаточным значением. Этот результат отчасти неожиданный: такой шаг всего в 5 раз меньше радиуса описанной возле атома сферы преимущественной локализации Ru 2p-волновой функции (см. выше). С другой стороны, не следует думать, что численное интегрирование можно заменить на сумму "всего по пяти точкам": так как интеграл (1) - трехмерный, то в итоге в "кубе" будет 5х5х5=125 точек при выбранном шаге.

Выводы.

В данной работе представлены доказательства адекватности использованных в [7] приближений для вычисления теоретических спектров XANES в рамках DFT. Так как только интегрирование по области где волновые функции возбуждаемых орбиталей рутения Ψ_2pk существенно отличаются от нуля приведет к вкладу в интегралы (1), было установлено, что интегрирование по трехмерной кубической сетке может быть сосредоточено только в небольшой области, охватывающей куб с ребром 0.45 Å вокруг поглотителя. Показано, что этого уже достаточно для покрытия области, содержащей более 99% электронной плотности орбиталей Ψ_2pk. Дополнительные тесты показали, что так действительно достигается сходимость по размеру сетки, и дальнейшее расширение области интегрирования не приводит к заметным спектральным изменениям. Аналогично, демонстрируется шаг интегрирования, при котором достигается сходимость формы изучаемых спектров.
Таким образом, проясняется вопрос, в каких пределах в [7] проводилось численное интегрирование и с каким шагом, что важно для аналогичных вычислений в будущем, поскольку трудоемкость расчетов растет пропорционально числу точек в охватываемой области.  Доказывается, что выбранные параметры позволяют достичь сходимости по форме изучаемых спектров XANES, и адекватны поставленной задаче.

Литература.

1.  Rehr J.J., Ankudinov A.L. Progress in the theory and interpretation of XANES// Coordination Chemistry Reviews. 2005. Т. 249. № 1-2. - C. 131-140.
2.  Smolentsev G., Soldatov A. Quantitative local structure refinement from XANES: multi-dimensional interpolation approach// Journal of Synchrotron Radiation. 2006. Т. 13. № 1. - C. 19-29.
3.  Groot F.d. Multiplet effects in X-ray spectroscopy// Coordination Chemistry Reviews. 2005. Т. 249. № 1-2. - C. 31-63.
4.  Groot F.d., Kotani A. X-Ray Absorption Spectroscopy // Core Level Spectroscopy of Solids  в 0 томах.: CRC Press, 2008. - C. 225-285
5.   Liu F., Concepcion J.J., Jurss J.W., Cardolaccia T., Templeton J.L., Meyer T.J. Mechanisms of Water Oxidation from the Blue Dimer to Photosystem II// Inorg. Chem. 2008. Т. 47. № 6. - C. 1727-1752.
6.  Velde G.T., Bickelhaupt F.M., Baerends E.J., Guerra C.F., Van Gisbergen S.J.A., Snijders J.G., Ziegler T. Chemistry with ADF// Journal of Computational Chemistry. 2001. Т. 22. № 9. - C. 931-967.
7.   Alperovich I., Smolentsev G., Moonshiram D., Jurss J.W., Concepcion J.J., Meyer T.J., Soldatov A., Pushkar Y. Understanding the Electronic Structure of 4d Metal Complexes: From Molecular Spinors to L-Edge Spectra of a di-Ru Catalyst// Journal of the American Chemical Society. 2011. Т. 133. № 39. - C. 15786-15794.