К вопросам построения эффективных алгоритмов расчета системы «сооружение-грунт»
Аннотация
Рассмотрено совместное использование МКЭ и МГЭ для расчета динамического поведения поверхностного сооружения на многослойном основании. Для реализации МГЭ при расчете основания предложен аналитический метод, эффективный при произвольном числе слоев и соотношений их параметров. Даны системы аппроксимирующих функций в области сопряжения методов, а также предложены формулы численного интегрирования на сопрягаемых элементах.
Ключевые слова: метод конечных элементов, метод граничных элементов, многослойное основание, фундаментальные решения.Ключевые слова:
При реализации методов расчета поведения поверхностных строительных объектов на основе совместного использования методов конечных (МКЭ) и граничных элементов (МГЭ) [1] важными вопросами являются построение эффективных схем расчета элементов напряженно-деформированного состояния полуограниченных структур, относящихся к многослойному основанию, и согласование методов в области их сопряжения.
- Для расчета основания предлагается метод полуплоскостей: как при определении полей от поверхностного источника, так и при нахождении фундаментальных решений для сосредоточенного источника с целью реализации МГЭ. Метод обладает высокой эффективностью, так как позволяет разделить волновые поля по их отражению от различных границ слоистой структуры, в том числе при анализе плотности потока энергии упругих колебаний.
Проиллюстрируем отмеченное на примере задачи плоской деформации многослойного полупространства.
Пусть область ![]() , занимаемая средой, представляет собой
, занимаемая средой, представляет собой ![]() -слойное упругое полупространство:
-слойное упругое полупространство: ![]() , описываемое в декартовой системе координат
, описываемое в декартовой системе координат ![]() как (рис. 1):
как (рис. 1):
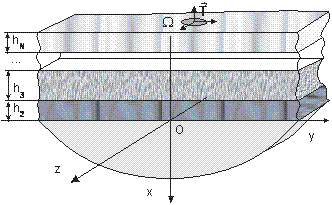
Рис. 1 – Область в декартовой системе координат
![]() – полупространство;
– полупространство;
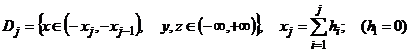 – j-й слой (j=2,...,N) толщины
– j-й слой (j=2,...,N) толщины ![]() .
.
Упругие свойства сред в ![]() описываются плотностью
описываются плотностью ![]() и коэффициентами Ламе
и коэффициентами Ламе ![]() или соответственно модулем упругости
или соответственно модулем упругости ![]() и коэффициентом Пуассона
и коэффициентом Пуассона ![]() :
:
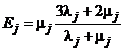 ,
,  .
.
На поверхности среды в области ![]() задана система распределенных усилий:
задана система распределенных усилий:
![]() .
.
В случае однородной полуплоскости с применением преобразования Фурье по переменной ![]()
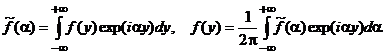
для функций перемещений точек данной области получим интегральные представления:
![]() . (1)
. (1)
Элементы матрицы ![]() имеют вид (
имеют вид (![]() ):
):
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
,
![]()
Аналогично для вектора напряжений на линиях ![]() , найдем, что
, найдем, что
![]() (2)
(2)
![]() ,
, 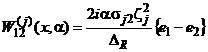
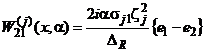 ,
, ![]() .
.
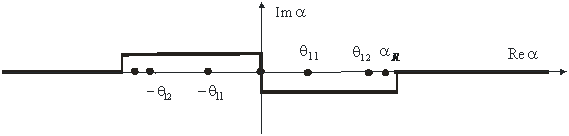
Рис. 2 – Контур интегрирования
Контур интегрирования ![]() в представлениях (1), (2) определяется применением принципа предельного поглощения [2]: при отсутствии диссипации энергии в среде обходит положительный корень уравнения Рэлея:
в представлениях (1), (2) определяется применением принципа предельного поглощения [2]: при отсутствии диссипации энергии в среде обходит положительный корень уравнения Рэлея: ![]() – снизу, отрицательный – сверху, а на остальной части совпадает с вещественной осью, как показано на рис. 2.
– снизу, отрицательный – сверху, а на остальной части совпадает с вещественной осью, как показано на рис. 2.
При наличии малой диссипации энергии в среде интегрирование можно проводить непосредственно по вещественной оси.
Решение для одного слоя при заданных на его гранях векторах напряжений:
![]() ,
, ![]()
строится способом суперпозиции решений для двух полуплоскостей.
Пусть в локальной системе координат для ![]() -го слоя:
-го слоя: ![]() амплитудные функции перемещений имеют вид:
амплитудные функции перемещений имеют вид:
![]() .
.
Функции ![]() , удовлетворяющие уравнениям движения, согласно предлагаемому методу будем разыскивать в виде суммы решений для полупространств
, удовлетворяющие уравнениям движения, согласно предлагаемому методу будем разыскивать в виде суммы решений для полупространств ![]() :
:
![]() . (3)
. (3)

Рис. 3
Здесь слагаемые ![]() в (3) являются решениями уравнений Ламе для однородной полуплоскости с удовлетворением граничных условий:
в (3) являются решениями уравнений Ламе для однородной полуплоскости с удовлетворением граничных условий:
![]() ,
, ![]() .
.
Вектор перемещений ![]() , представим через трансформанты вектора напряжений
, представим через трансформанты вектора напряжений ![]() в виде:
в виде:
![]() . (4)
. (4)
Здесь функции ![]() получены из
получены из ![]() заменой упругих параметров полуплоскости на параметры
заменой упругих параметров полуплоскости на параметры ![]() -го слоя.
-го слоя.
Аналогично формуле (4) определяются перемещения для полуплоскости ![]() через функции
через функции ![]() , где для элементов
, где для элементов ![]() справедливы соотношения:
справедливы соотношения:
![]() ,
, ![]() ,
, ![]() – символ Кронекера.
– символ Кронекера.
Определяя напряженное состояние слоя в виде суммы соответствующих решений для двух полуплоскостей, получим:
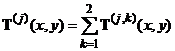 , (5)
, (5)
где ![]() имеют вид (2).
имеют вид (2).
Для второй группы слагаемых найдем: ![]() .
.
При рассмотрении далее общей краевой задачи для ![]() -слойной полуплоскости используются граничные условия и условия сцепления слоев между собой и подстилающей полуплоскостью, что в пространстве преобразований Фурье по переменной
-слойной полуплоскости используются граничные условия и условия сцепления слоев между собой и подстилающей полуплоскостью, что в пространстве преобразований Фурье по переменной ![]() приводит к системе ЛАУ относительно неизвестных функций напряжений
приводит к системе ЛАУ относительно неизвестных функций напряжений ![]() ,
, ![]() ;
; ![]() .
.
По найденным компонентам напряжений на гранях слоя можно восстановить осредненный за период колебаний поток энергии, проходящий через границы раздела сред ![]() :
:
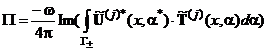 . (6)
. (6)
Здесь, при введении малой диссипации в слоях конструкции в качестве контура ![]() выбиралась вещественная ось.
выбиралась вещественная ось.
Подставляя далее выражения (3), (5) в преобразованном по Фурье виде в соотношение (6), получим:

 , где
, где ![]() имеют смысл плотности потока энергии излучаемых и отраженных волн от плоской поверхности
имеют смысл плотности потока энергии излучаемых и отраженных волн от плоской поверхности ![]() .
.
- Важным моментом при численной реализации совместного использования методов конечных и граничных элементов для системы «сооружение-грунт» является выбор системы аппроксимирующих функций, а также применение формул численного интегрирования на элементах.
Стыковка МКЭ и МГЭ предполагает равенство векторов узловых перемещений и усилий в области контакта ![]() фундамента здания или сооружения и окружающего грунтового массива и не требует согласования данных характеристик вне узлов. Отсюда выбор закона полиномиального распределения перемещений в области контакта может быть независимым для каждого из методов (безусловно, предпочтительнее выбирать аппроксимирующие функции одной и той же степени).
фундамента здания или сооружения и окружающего грунтового массива и не требует согласования данных характеристик вне узлов. Отсюда выбор закона полиномиального распределения перемещений в области контакта может быть независимым для каждого из методов (безусловно, предпочтительнее выбирать аппроксимирующие функции одной и той же степени).
Не ограничивая общности, можно считать, что область контакта ![]() является плоской с введением локальной системы координат
является плоской с введением локальной системы координат ![]() . Соответствующая система узлов
. Соответствующая система узлов ![]() определяется разбиением конечной части системы «сооружение-грунт» в методе конечного элемента и выбором типа конечного элемента.
определяется разбиением конечной части системы «сооружение-грунт» в методе конечного элемента и выбором типа конечного элемента.
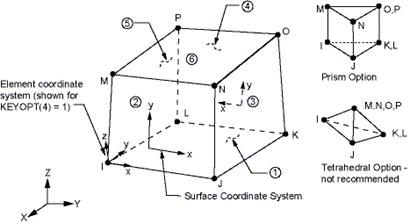
Рис. 4
Так для восьмиузловых твердотельных элементов (рис. 4) область ![]() разбивается на четырехугольные граничные элементы (IJKL). При использовании опции элементов: призма или тетраэдр, граничные элементы имеют форму треугольников (IJK). Таким образом, наиболее общей формой граничных элементов для применения МГЭ является треугольная. К этому же приводит разбиение области контакта неплоской формы путем триангуляции соответствующей поверхности в пространстве.
разбивается на четырехугольные граничные элементы (IJKL). При использовании опции элементов: призма или тетраэдр, граничные элементы имеют форму треугольников (IJK). Таким образом, наиболее общей формой граничных элементов для применения МГЭ является треугольная. К этому же приводит разбиение области контакта неплоской формы путем триангуляции соответствующей поверхности в пространстве.
Таким образом, считаем, что область ![]() разбита сетью граничных треугольных элементов с узлами
разбита сетью граничных треугольных элементов с узлами ![]() В каждом узле вектор перемещений
В каждом узле вектор перемещений ![]() имеет значение
имеет значение ![]() ,
, ![]() .
.

Рис. 5
Применим на элементе линейную аппроксимацию:
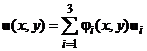 ,
, ![]() (7)
(7)
Константы ![]() определяются из условий
определяются из условий ![]() ,
, ![]() - символ Кронекера. В результате получим:
- символ Кронекера. В результате получим:
![]() , (8)
, (8)
![]() ,
,
![]() ,
,
![]() .
.
Следует отметить, что линейная интерполяция неизвестной функции на каждом элементе не нарушает условия непрерывности поля перемещений в целом на границе ![]() . Это следует из условий равенства полного набора констант аппроксимации для области
. Это следует из условий равенства полного набора констант аппроксимации для области ![]() (
(![]() , где
, где ![]() - число граничных элементов модели) и суммы числа условий непрерывности перемещений в узлах для смежных элементов и числа самих узлов как точек коллокации для определения неизвестных перемещений в них.
- число граничных элементов модели) и суммы числа условий непрерывности перемещений в узлах для смежных элементов и числа самих узлов как точек коллокации для определения неизвестных перемещений в них.
При использовании аппроксимаций более высокого порядка, например квадратичной (лагранжевы элементы), условия согласования перемещений в узлах и их корректное определение требуют введения дополнительных узлов по центру сторон треугольников. Это в свою очередь приводит к необходимости использования в сопрягаемом МКЭ 10-узловых пирамидальных элементов (рис. 6), что увеличивает порядок системы линейных уравнений метода конечных элементов и сложности стыковки с МГЭ. Получаемое же увеличение точности решения легко можно компенсировать уменьшением сетки разбиения при использовании линейной интерполяции на элементах.
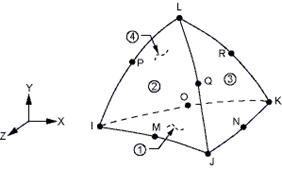
Рис. 6
Решение граничного интегрального уравнения требует также аппроксимации в области ![]() вектора напряжений:
вектора напряжений:
![]() , где
, где ![]() - тензор напряжений Коши,
- тензор напряжений Коши, ![]() - нормаль к области
- нормаль к области ![]() . Исходя из требования сохранения количества узлов сопрягаемых сеток граничных и конечных элементов, для вектора напряжений необходимо применять интерполирующие функции того же порядка, что и для вектора перемещений.
. Исходя из требования сохранения количества узлов сопрягаемых сеток граничных и конечных элементов, для вектора напряжений необходимо применять интерполирующие функции того же порядка, что и для вектора перемещений.
Форма сопряжения МГЭ и МКЭ по напряжениям в узловых точках в этом случае может иметь следующий вид:
![]() ,
,
здесь ![]() - узловое усилие в
- узловое усилие в ![]() -м узле МКЭ;
-м узле МКЭ;
![]() - значение вектора напряжений в
- значение вектора напряжений в ![]() -м узле МГЭ;
-м узле МГЭ;
![]() - множество граничных элементов, сопряженных с
- множество граничных элементов, сопряженных с ![]() -м узлом;
-м узлом;
![]() - площадь элемента с номером
- площадь элемента с номером ![]() (рис. 5),
(рис. 5), 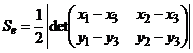 ;
;
![]() - количество узлов граничного элемента (в случае линейной интерполяции
- количество узлов граничного элемента (в случае линейной интерполяции ![]() , для квадратичной -
, для квадратичной - ![]() ).
).
При использовании метода граничных элементов необходимым элементом является интегрирование по двумерной области с разбиением на треугольные элементы:
![]() ,
,
где подынтегральная функция ![]() может иметь интегрируемую особенность степенного или логарифмического характера в точках
может иметь интегрируемую особенность степенного или логарифмического характера в точках ![]() , совпадающих с узлами аппроксимации (вершинами треугольника или серединами его сторон). В этом случае одним из способов интегрирования, показавшим существенную эффективность, является использование квадратурных формул с узлами внутри треугольной области.
, совпадающих с узлами аппроксимации (вершинами треугольника или серединами его сторон). В этом случае одним из способов интегрирования, показавшим существенную эффективность, является использование квадратурных формул с узлами внутри треугольной области.
Отобразим треугольник ![]() (рис. 5):
(рис. 5): ![]() , на равносторонний треугольник
, на равносторонний треугольник ![]() в системе координат
в системе координат ![]() (рис.7) с использованием линейного преобразования:
(рис.7) с использованием линейного преобразования:
![]() .
.

Рис. 7
Несложно получить, что
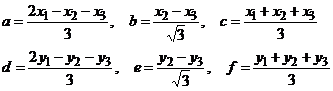 .
.
В результате имеем:
![]() ,
,
 - якобиан перехода к системе координат
- якобиан перехода к системе координат ![]() .
.
Для вычисления двойного интеграла по треугольнику ![]() воспользуемся 7-узловой квадратурной формулой:
воспользуемся 7-узловой квадратурной формулой:
 ,
,
где весовые коэффициенты ![]() и узлы
и узлы ![]() приведены в таблице 1.
приведены в таблице 1.
Таблица 1.
i |
|
|
|
|
1 |
270/1200 |
0 |
0 |
|
2 |
|
|
0 |
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
0 |
|
6 |
|
|
|
|
7 |
|
|
|
Данная формула имеет 6 порядок точности: ![]() [3].
[3].
Литература
- 1.Кадомцев, М.И.Исследование динамики заглубленных фундаментов методами граничных и конечных элементов / Кадомцев, М.И., Ляпин, А.А., Селезнев, М.Г. // Строительная механика и расчет сооружений. – 2010. – № 3. – С.61–64.
2.Бабешко, В.А.Динамика неоднородных линейно-упругих сред / Бабешко, В.А., Глушков, Е.В., Зинченко, Ж.З./ – М. : Наука; Главная редакция физико-математической литературы. 1989. – 343 с.
3.Справочник по специальным функциям /Под ред. М.Абрамовица и И.Стиган/ -М.: Наука, 1979. –832 с