Математическая модель деформирования подкрепленных оболочек вращения при учете различных свойств материала
Аннотация
Математическая модель учитывает геометрическую и физическую нелинейности, возможность развития деформации ползучести. Работа ребер учитывается с помощью метода конструктивной анизотропии, но с учетом сдвиговой и крутильной жесткости. При решении физически-нелинейных задач секущий модуль определяется непосредственно из кривой «σ-ε», найденной опытным путем. Математическая модель записана в виде функционала полной энергии деформации. Такая модель может быть использована для комплексного исследования устойчивости подкрепленных оболочек вращения.
Ключевые слова: устойчивость подкрепленных оболочек вращения, линейно-упругие задачи, нелинейно-упругие задачи, задачи ползучести.Ключевые слова:
05.13.18 - Математическое моделирование, численные методы и комплексы программ
При деформировании срединной поверхности оболочки все точки получат перемещения. Связь деформаций через перемещения – геометрические соотношения теории оболочек – в срединной поверхности принимают вид [1]
![]()
![]()
![]()
где
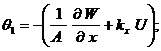
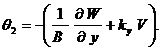
Кроме того, если учитываются поперечные сдвиги (модель Тимошенко – Рейснера), то
![]()
![]()
Здесь ![]() – функция, характеризующая распределение напряжений
– функция, характеризующая распределение напряжений ![]() по толщине оболочки; A,B – параметры Ляме.
по толщине оболочки; A,B – параметры Ляме.
Деформации в точках, расположенных на расстоянии z от координатной поверхности, выражаются соотношениями
![]()
![]()
где функции изменения кривизн ![]() и кручения
и кручения ![]() принимают вид
принимают вид
![]()
![]()
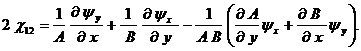
Физические соотношения (связь напряжений и деформаций) для упругого изотропного материала оболочки на основе закона Гука будут иметь вид
![]()
![]()
![]()
Физические соотношения на основе деформационной теории пластичности имеют вид [2][3]
![]()
![]()
![]()
где Ec-секущий модуль упругости.
Физические соотношения при учете ползучести материала на основе линейной теории наследственной ползучести принимают вид [4]
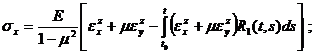
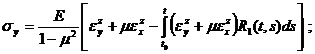
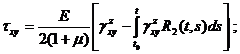
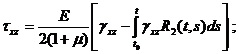
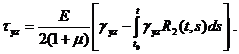
Здесь ![]() – функции влияния (ядра релаксации) материала при растяжении и сдвиге.
– функции влияния (ядра релаксации) материала при растяжении и сдвиге.
Если ребра вводятся по методу конструктивной анизотропии (при этом ребра должны быть часто расположены), то функционал полной энергии деформации оболочки, независимо от проявляемых свойств материала можно записать в виде
![]()
![]()
![]() (1)
(1)
Здесь ![]() - компоненты внешней нагрузки вдоль осей
- компоненты внешней нагрузки вдоль осей ![]() .
.
Если решается линейно-упругая задача, то усилия и моменты имеют вид [5]
![]()
![]()
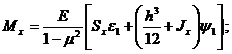
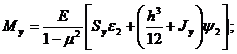
![]()
![]()
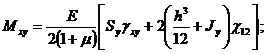
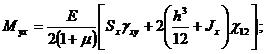
![]()
![]()
Здесь ![]()
![]()
![]()
Приведенные жесткостные характеристики ребер с учетом сдвиговой и крутильной жесткости имеют вид
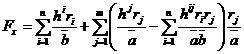 ;
;
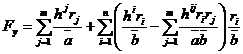 ;
;
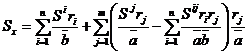 ;
;
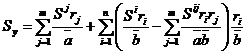 ;
;
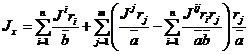 ;
;
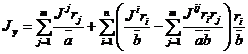 ,
,
где
![]()
![]()
![]()
![]()
![]()
![]()
![]()
При решении нелинейно-упругих задач обычно секущий модуль упругости, исходя из зависимости «![]() », аппроксимируется некоторым аналитическим выражением.
», аппроксимируется некоторым аналитическим выражением.
Аппроксимация секущего модуля в виде![]() , когда
, когда ![]() , справедлива при малой нелинейности кривой «
, справедлива при малой нелинейности кривой «![]() », полученной экспериментально для конкретного материала при одноосном растяжении.
», полученной экспериментально для конкретного материала при одноосном растяжении.
При решении задач устойчивости подкрепленных оболочек вращения наиболее точная аппроксимация кривой «![]() » может быть получена, если кривая «
» может быть получена, если кривая «![]() » (при сложном напряженном состоянии – это «
» (при сложном напряженном состоянии – это «![]() ») задана характерными точками и по численному заданию графика «
») задана характерными точками и по численному заданию графика «![]() » при полученном значении
» при полученном значении ![]() (найденном на предыдущей итерации, так как при решении физически-нелинейных задач удобно применять метод упругих решений А.А. Ильюшина) находится
(найденном на предыдущей итерации, так как при решении физически-нелинейных задач удобно применять метод упругих решений А.А. Ильюшина) находится ![]() и за секущий модуль в точке с координатами
и за секущий модуль в точке с координатами ![]() берется
берется
![]()
![]()
Заметим, что ![]() , поэтому при изменении
, поэтому при изменении ![]() меняется и
меняется и ![]() , найденное из графической зависимости «
, найденное из графической зависимости «![]() ».
».
Таким образом, при вычислении интегралов по ![]() в функционале (1) необходимо при каждом значении
в функционале (1) необходимо при каждом значении ![]() и
и ![]() вычислять интеграл по переменной
вычислять интеграл по переменной ![]() .
.
Если решается нелинейно-упругая задача, то усилия и моменты можно представить в виде
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Здесь ![]()
![]()
![]()
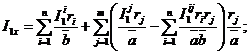
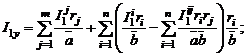
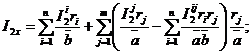
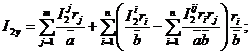
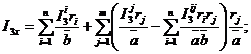
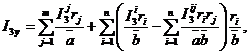
где
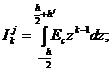
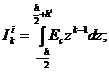
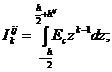
k=1, 2, 3.
Если решается задача ползучести, то
![]()
![]()
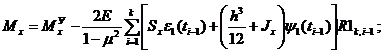
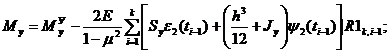
![]()
![]()
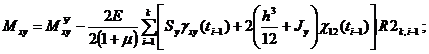
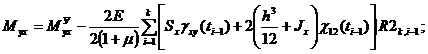
![]()
![]()
Здесь ![]()
Например, для оргстекла
![]()
где ![]()
![]()
и тогда
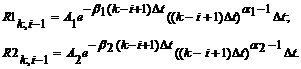
Для старого бетона
![]()
где
![]()
и тогда ![]()
Литература:
1.Новожилов В. В. Теория тонких оболочек. – Л.: Судпромиздат, 1962. – 431 с.
2.Вольмир А.С. Нелинейная динамика пластинок и оболочек. – М.: Наука, 1972. – 432 с.
3.Качанов Л.М. Основы теории пластичности. М.: Наука, 1969. – 420 с.
4.Ржаницын А. Р. Строительная механика. - М.: Высшая школа. 1982. – 400 с.
5.Карпов В.В. Математическое моделирование, алгоритмы исследования модели, вычислительный эксперимент в теории оболочек. –СПб.: СПбГАСУ, 2006. – 330 с.