Сравнительный анализ результатов моделирования пористой пьезокерамики методами эффективных модулей и конечных элементов с экспериментальными данными
Аннотация
Дата поступления статьи: 15.04.2013Представлены результаты вычислительных экспериментов по определению характеристик пористой пьезокерамики по методологии, включающей метод эффективных модулей, моделирование представительных объемов по простому случайному методу и по методу Виттена-Сандера, метод конечных элементов для решения статических задач электроупругости для неоднородных композитных сред и учет неоднородности поляризации вблизи пор. Проведено сравнение результатов компьютерного моделирования с известными экспериментальными данными для пористого материала PZT-4 и его аналогов. Сделан вывод, что учет неоднородности поляризации в окрестности пор обеспечивает лучше согласование полученных численных результатов с большим числом известных экспериментальных данных. При этом, для большинства эффективных констант наименьшая погрешность получена на представительных объемах пористого пьезокерамического материала, построенных по методу Виттена-Сандера.
Ключевые слова: пьезокомпозит, пористая пьезокерамика, неоднородная поляризация, математическое моделирование, модели представительных объемов, метод конечных элементов, эффективные модули
01.04.07 - Физика конденсированного состояния
05.13.18 - Математическое моделирование, численные методы и комплексы программ
В ряде исследований [1–3] отмечалась перспективность использования пористой пьезокерамики в качестве активных элементов пьезопреобразователей для различных акустических применений. Эффективность пористой пьезокерамики во многом определяется ее высокой объемной пьезочувствительностью, широкополосностью и более меньшим импедансом в сравнении с плотной пьезокерамикой.
В данной работе представлены результаты вычислительных экспериментов по определению характеристик пористой пьезокерамики по методологии, включающей метод эффективных модулей, моделирование представительных объемов, метод конечных элементов для решения статических задач электроупругости для неоднородных композитных сред и учет неоднородности поляризации вблизи пор. Основы данной методологии восходят к работам [4, 5], а применительно к приводимым ниже расчетам подробно описаны в [6, 7].
Актуальность компьютерного моделирования определяется не только важностью пористой пьезокерамики для акустических применений, но и тем, что имеющиеся экспериментальные данные по свойствам пористой пьезокерамики достаточно противоречивы, и зависимости эффективных констант, представленные в различных работах, зачастую достаточно сильно отличаются [1–16]. Кроме того, экспериментальные данные по модулям пьезокерамики фактически являются экспериментально-аналитическими, так как они получаются в результате использования собственно экспериментальных данных, а также аналитических формул, полученных для упрощенных канонических задач электроупругости [17], причем выведенных для плотных пьезокерамических материалов.
Авторами были проведены многочисленные вычислительные эксперименты по определению эффективных модулей пористых пьезокерамических материалов различной сегнетожесткости [1, 18] с учетом и без учета гипотезы о неоднородности поля поляризации в окрестности пор. Конечно-элементные модели представительных объемов пористых пьезокерамик состояли из кубических решеток геометрически одинаковых ячеек – кубиков. Для генерирования пор использовались два метода, описанные в [7]: простой случайный метод и метод ограниченной диффузией агрегации Виттена-Сандера. При небольшом проценте пористости в качестве достаточно простой и адекватной модели пьезокерамической кубической решетки можно использовать модель, состоящую из одинаковых ячеек – кубиков, часть из которых случайным образом объявляется порами (простой случайный метод). Однако такая модель при большом числе пор может терять связность каркаса и не поддерживать связность структуры композита (3-0 или 3-3). Для построения связанных структур в кубической решетке использовался алгоритм теории перколяции Виттена-Сандера [7], позволяющий получать протекающие кластеры. При малой пористости он может использоваться для построения кластеров из пор, а при большой пористости – кластеров из пьезокерамического материала.
Сравнение результатов расчетов с экспериментальными данными, проведем на примере пористого материала средней сегнетожесткости PZT-4 и его аналогов, данные по которому представлены в [1, 2, 8, 9, 10–14]. На всех приводимых ниже графиках синие линии соответствуют зависимостям, полученным для представительного объема, сгенерированного простым случайным методом, а красные – методом Виттена-Сандера. При этом зависимости, полученные без учета неоднородности поля поляризации, помечены кружками; треугольники соответствуют расчетам с учетом неоднородной поляризации; а экспериментальные данные обозначены ромбами.
На рис. 1 показана зависимость относительной диэлектрической проницаемости ![]() от пористости
от пористости ![]() в сравнении с экспериментальными данными [11, 12]. Исходя из графиков, приведенных на рис. 1, можно сделать вывод, что как для простого случайного метода генерации представительного объема, так и для метода Виттена-Сандера, зависимости
в сравнении с экспериментальными данными [11, 12]. Исходя из графиков, приведенных на рис. 1, можно сделать вывод, что как для простого случайного метода генерации представительного объема, так и для метода Виттена-Сандера, зависимости ![]() носят линейный характер. При этом результаты, полученные с учетом гипотезы о неоднородности поля поляризации, отличаются от данных, полученных без учета данной гипотезы, не более, чем на 1-2%. Видно, что все четыре зависимости очень близки, и численные результаты лучше согласуются с данными из [11]. Значения, полученные в [12], убывают сильнее с ростом пористости, давая уже при 38% пористости расхождение с расчетными данными и результатами [11] порядка 35%.
носят линейный характер. При этом результаты, полученные с учетом гипотезы о неоднородности поля поляризации, отличаются от данных, полученных без учета данной гипотезы, не более, чем на 1-2%. Видно, что все четыре зависимости очень близки, и численные результаты лучше согласуются с данными из [11]. Значения, полученные в [12], убывают сильнее с ростом пористости, давая уже при 38% пористости расхождение с расчетными данными и результатами [11] порядка 35%.
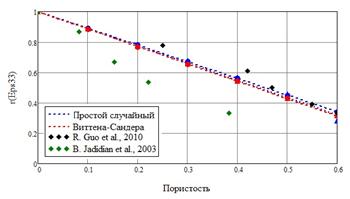
Рис. 1. – Зависимости относительной диэлектрической проницаемости от пористости
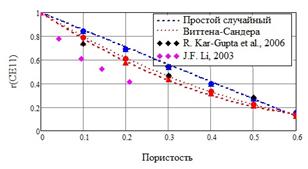
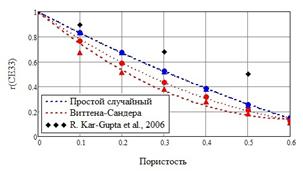
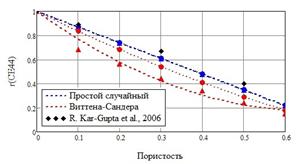
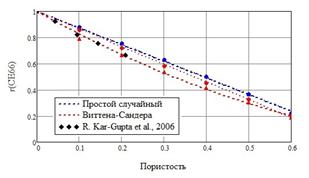
На рис. 2 приведены зависимости, полученные для упругих модулей, в сравнении с экспериментальными данными из [13, 14]. Зависимости относительного упругого модуля ![]() хорошо аппроксимируются линейными функциями от пористости в случае простого случайного метода генерации представительного объема; а зависимости, соответствующие методу Виттена-Сандера, носят квадратичный характер. Можно отметить, что характер зависимостей не изменяется с учетом гипотезы о неоднородности поляризации; однако, данные, полученные с учетом этой гипотезы, и соответствующие второму методу генерации пор, лучше других согласуются с экспериментальными, полученными в [13]. Представленные в [14] экспериментальные зависимости модуля
хорошо аппроксимируются линейными функциями от пористости в случае простого случайного метода генерации представительного объема; а зависимости, соответствующие методу Виттена-Сандера, носят квадратичный характер. Можно отметить, что характер зависимостей не изменяется с учетом гипотезы о неоднородности поляризации; однако, данные, полученные с учетом этой гипотезы, и соответствующие второму методу генерации пор, лучше других согласуются с экспериментальными, полученными в [13]. Представленные в [14] экспериментальные зависимости модуля ![]() с ростом пористости
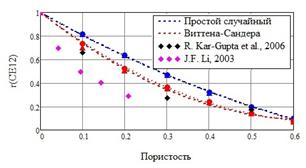
с ростом пористости ![]() также убывают по квадратичному закону, однако, в этом случае расхождение с данными [13] и результатами численных экспериментов составляет не менее 25%. Для модулей
также убывают по квадратичному закону, однако, в этом случае расхождение с данными [13] и результатами численных экспериментов составляет не менее 25%. Для модулей ![]() ,
, ![]() и
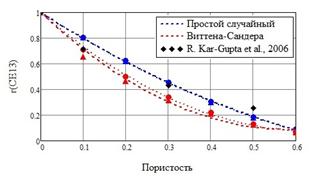
и ![]() при обоих способах построения представительного объема пористой структуры, а также с учетом и без учета неоднородности поляризации, получены квадратичные зависимости модулей от пористости. Наименьшая погрешность модуля
при обоих способах построения представительного объема пористой структуры, а также с учетом и без учета неоднородности поляризации, получены квадратичные зависимости модулей от пористости. Наименьшая погрешность модуля ![]() в сравнении с экспериментальными данными [13] наблюдается при учете неоднородности поляризации и с использованием метода Виттена-Сандера. При построении зависимостей
в сравнении с экспериментальными данными [13] наблюдается при учете неоднородности поляризации и с использованием метода Виттена-Сандера. При построении зависимостей ![]() и
и ![]() от пористости данные, лучше согласующиеся с экспериментальными, получены при использовании простого случайного метода генерации представительного объема. Однако стоит отметить, что погрешность при определении модуля
от пористости данные, лучше согласующиеся с экспериментальными, получены при использовании простого случайного метода генерации представительного объема. Однако стоит отметить, что погрешность при определении модуля ![]() составила не более 10%, тогда как для модуля
составила не более 10%, тогда как для модуля ![]() она превысила 40% уже при значении p=0.5.
она превысила 40% уже при значении p=0.5.
Линейная зависимость относительного упругого модуля ![]() , полученная при простом случайном методе, показала наилучшее соответствие экспериментальным данным [13], и при этом максимальная погрешность составила не более 7%. Упругий модуль
, полученная при простом случайном методе, показала наилучшее соответствие экспериментальным данным [13], и при этом максимальная погрешность составила не более 7%. Упругий модуль ![]() изменялся по линейному закону для первого метода генерации пор. Однако, зависимость, лучше всего соответствующая экспериментальным данным, была получена в случае метода Виттена-Сандера и при учете неоднородности поля поляризации; максимальная погрешность не превышала 2-3%, тогда как данные, соответствующие простому случайному методу показали отклонение от экспериментальных более, чем на 20%.
изменялся по линейному закону для первого метода генерации пор. Однако, зависимость, лучше всего соответствующая экспериментальным данным, была получена в случае метода Виттена-Сандера и при учете неоднородности поля поляризации; максимальная погрешность не превышала 2-3%, тогда как данные, соответствующие простому случайному методу показали отклонение от экспериментальных более, чем на 20%.
а) б)
в) г)
д) е)
Рис. 2. – Зависимости относительных упругих модулей от пористости
После вычисления полных наборов эффективных модулей ![]() ,
, ![]() ,
, ![]() находились такие важнейшие характеристики пьезокерамики, как пьезомодули деформаций
находились такие важнейшие характеристики пьезокерамики, как пьезомодули деформаций ![]() , где
, где ![]() – компоненты матрицы упругих податливостей (обратной к матрице упругих жесткостей). Будем рассматривать их относительные изменения
– компоненты матрицы упругих податливостей (обратной к матрице упругих жесткостей). Будем рассматривать их относительные изменения ![]() , где
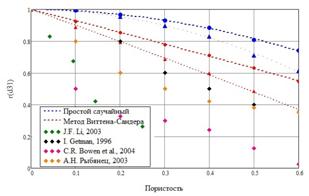
, где ![]() . Проанализируем графики зависимостей продольного (рис. 3, а) и поперечного (рис. 3, б) пьезомодулей деформаций, представленные ниже, и сравним их с экспериментальными зависимостями из [3, 5, 10, 12, 14]. На рис. 3, а приведены зависимости относительных величин пьезомодуля
. Проанализируем графики зависимостей продольного (рис. 3, а) и поперечного (рис. 3, б) пьезомодулей деформаций, представленные ниже, и сравним их с экспериментальными зависимостями из [3, 5, 10, 12, 14]. На рис. 3, а приведены зависимости относительных величин пьезомодуля ![]() от пористости в сравнении с экспериментальными данными [3, 5, 10, 12, 14].
от пористости в сравнении с экспериментальными данными [3, 5, 10, 12, 14].
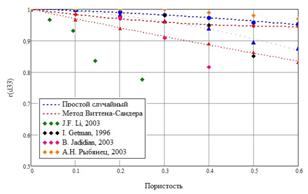
а) б)
Рис. 3. – Зависимости относительных пьезомодулей от пористости
Как видно, при методе Виттена-Сандера с ростом пористости наблюдается более значительное убывание пьезомодуля ![]() , чем при простом случайном методе. Необходимо отметить, что зависимость, полученная в предположении неоднородной поляризации пьезокерамической матрицы для метода Виттена-Сандера, лучше других согласуется с данными эксперимента. В то же время величины пьезомодуля
, чем при простом случайном методе. Необходимо отметить, что зависимость, полученная в предположении неоднородной поляризации пьезокерамической матрицы для метода Виттена-Сандера, лучше других согласуется с данными эксперимента. В то же время величины пьезомодуля ![]() практически не зависят от пористости для обоих методов (рис. 3, б). Однако учет гипотезы о неоднородности поля поляризации вызывает более быстрый спад зависимостей; что лучше соответствуют некоторым из экспериментальных данных. Следует отметить, что максимальная погрешность остается довольно существенной и составляет, приблизительно, 10-15% для данных [10, 12, 14], и порядка 3-5% для данных [3, 5].
практически не зависят от пористости для обоих методов (рис. 3, б). Однако учет гипотезы о неоднородности поля поляризации вызывает более быстрый спад зависимостей; что лучше соответствуют некоторым из экспериментальных данных. Следует отметить, что максимальная погрешность остается довольно существенной и составляет, приблизительно, 10-15% для данных [10, 12, 14], и порядка 3-5% для данных [3, 5].
Из представленных на рис. 1–3 результатов вычислительных экспериментов можно заключить, что учет неоднородности поляризации в окрестности пор (см. также [19]) обеспечивает лучше согласование полученных зависимостей с большим числом известных экспериментальных данных [1–5, 8–16]. При этом, для большинства эффективных констант наименьшая погрешность была получена на представительных объемах пористого пьезокерамического материала, построенных по методу Виттена-Сандера, что позволяет признать его лучшие возможности описания пористых структур в сравнении с простым случайным методом.
Работа выполнена при финансовой поддержке РФФИ в рамках научных проектов № 13-01-00943 (в части исследований по моделированию представительных объемов) и № 12-08-31350 (в части исследований по компьютерному моделированию эффективных свойств пористой пьезокерамики для гидроакустических применений).
Литература:
- Лопатин С.С., Лупейко Т.Г. Свойства пористой пьезоэлектрической керамики типа цирконата-титаната свинца [Текст] // Изв. АН СССР. Сер. Неорг. Матер., 1991. – Т. 27, № 9. – С. 1948-1951.
- Данцигер А.Я., Разумовская О.Н., Резниченко Л.А. и др. Многокомпонентные системы сегнетоэлектрических сложных оксидов: физика, кристаллохимия, технология. Аспекты дизайна пьезоэлектрических материалов [Текст] – Ростов н/Д: Изд-во Рост. ун-та, 2002. – Т. 2. – 365 с.
- Рыбянец А.Н., Мирошниченко Е.С., Макарьев Д.И., Маяк Г.М., Федорук В.И. Пористая пьезокерамика. История и перспективы применения [Текст] // Пьезотехника-2003. Материалы Межд. научно-практич. конф. «Фундамент. проблемы пьезоэлектрич. приборостроения». Москва, 26-29 ноября 2003 г. – Москва: МИРЭА, 2003. – С.99-104.
- Хорошун Л.Н., Маслов Б.П., Лещенко П.В. Прогнозирование эффективных свойств пьезоактивных композитных материалов [Текст] – Киев : Наукова Думка, 1989. – 347 с.
- Getman I., Lopatin S. Theoretical and experimental investigation of the porous PZT ceramics [Текст] // Ferroelectrics, 1996. – V. 186. – P. 301-304.
- Nasedkin A.V., Shevtsova M.S. Improved finite element approaches for modeling of porous piezocomposite materials with different connectivity [Текст] / Ferroelectrics and Superconductors: Properties and Applications. Ed. I.A. Parinov. N.-Y.: Nova Science Publishers, 2011. – Ch. 7. – P. 231–254.
- Domashenkina T.V., Nasedkin A.V., Remizov V.V., Shevtsova M.S. Finite element modeling of porous piezocomposite materials with different connectivity and applications for analysis of ultrasonic transducers [Электронный ресурс] // Proc. 7th GRACM Int. Congr. Comput. Mech., Athens, Greece, June 30 – July 2, 2011. – CD. – Paper 141. 10 p.
- Сегалла А.Г., Соловьев М.А., Галанов Г.Н., Сафронов А.Я., Голова Л.В. Изготовление и исследование ряда пористых пьезокерамических материалов связности 3-0 [Текст] // Пьезотехника-2005. Материалы Межд. научно-практич. конф. «Фунд. пробл. функционального материаловедения, пьезоэлектрич. приборостроения и нанотехнологий». Ростов-на-Дону, Азов, 23-26 августа 2005 г. – Ростов-на-Дону: РГПУ, 2005. – С. 220-223.
- Ситало Е.И., Еремкин В.В., Смотраков В.Г., Цихоцкий Е.С. Электроупругие свойства высокопористой сегнетокерамики [Текст] // Там же. – С. 204-206.
- Bowen C.R., Perry A., Lewis A.C.F., Kara H. Processing and properties of porous piezoelectric materials with high hydrostatic figures of merit [Текст] // Journal of the European Ceramic Society, 2004. – № 24. – P. 541-545.
- Guo R., Wang C.-A. Enhanced piezoelectric property of porous lead zirconate titanate ceramics with one dimensional ordered pore structure [Текст] // Journal of Applied Physics, 2010. – № 108. – P. 124112 1-4.
- Jadidian B., Winder A. Porous piezoelectric ceramics with 0-3 connectivity [Электронный ресурс] // http://www.jwmed.com/docs.htm
- Kar-Gupta R., Venkatesh T.A. Electromechanical response of porous piezoelectric materials [Текст] // Acta Materialia, 2006. – №54. – P. 4063-4078.
- Li J.F., Takagi K., Ono, M., Pan W., Watanabe R. Fabrication and evaluation of porous piezoelectric ceramics and porosity-graded piezoelectric actuators [Текст] // J. Am. Ceram. Soc., 2003. – V. 86. – P. 1094-1098.
- Zeng T., Dong X.L., Mao C.L., Zhou Z.Y., Yang H. Effects of pore shape and porosity on the properties of porous PZT 95/5 ceramics [Текст] // Journal of the European Ceramic Society, 2007. – № 27. – P. 2025-2029.
- Zhang H.L., Li J.-F., Zhang B.-P. Microstructure and electrical properties of porous PZT ceramics derived from different pore-forming agents [Текст] // Acta Materialia, 2007. – № 55. – P. 171-181.
- Земляков В.Л., Ключников С.Н. Определение пьезомодуля материала пьезокерамического элемента [Текст] // Инженерный вестник Дона, 2012. – Т: 20

 , № 2. – С. 374-384.
, № 2. – С. 374-384. - Панич А.А., Мараховский М.А., Мотин Д.В. Кристаллические и керамические пьезоэлектрики [Текст] // Инженерный вестник Дона, 2011. – Т: 15
 , № 1. – С. 53-64.
, № 1. – С. 53-64. - Вернигора Г.Д., Лупейко Т.Г., Скалиух А.С., Соловьев А.Н. О поляризации и определении эффективных характеристик пористой пьезокерамики [Текст] // Вестник ДГТУ, 2011. – Т. 11. № 4 (55). – С. 462-469.