Оценка точности определения влажной составляющей поправки в расстояния

Аннотация

В.И. Куштин

Выполнено исследование точности определения поправок в расстояния, измеряемые радиоэлектронными системами, за влажную составляющую индекса преломления. Получены оригинальные формулы определения поправок за влажную составляющую в наклонные расстояния.

Ключевые слова: Атмосфера, Индекс преломления, Влажная составляющая, Поправка в дальность

25.00.32 - Геодезия

Для наклонного расстояния поправку  ΔS_В  за влажную составляющую определяют по формуле [1]

 .                               (1)

Выполняя численное интегрирование по формуле Симпсона, находим

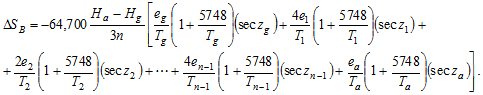  (2)

Используя формулу средней квадратической ошибки функции независимых аргументов, находим

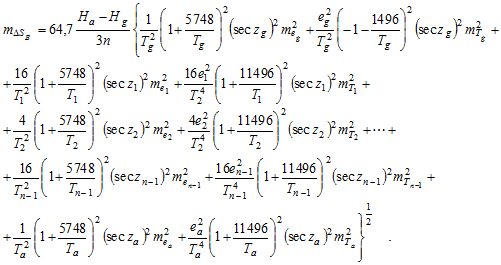(3)

При наземных измерениях ошибка измерения температуры равна  ±0,1⁰С, относительной влажности – 1%, а при радиозондовых наблюдениях  ±1⁰С и 5% соответственно. Положим, что эти ошибки равны средним квадратическим ошибкам.

Выполненные исследования  для пункта с высокой влажностью (ГОСТ 26352-84, Панама, июль) при  z_g = 0⁰, показали, что значения 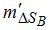 , вычисленные без учета ошибки определения температуры, практически совпадают с  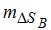, полученными с учетом этой ошибки. Поэтому слагаемые с  m_T²  в формуле (3) можно не учитывать. При  Н > 6 км значения  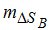практически не изменяются. Учитывая эти обстоятельства, вместо(3),получаем

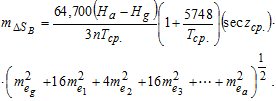                             (4)

Подставляя в формулу (4)  Н_а – H_g = 6 км,  n = 6, 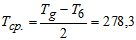 К,  z_cp. = 0  и значения  m_e  до 6 км, имеем  = 7,9 мм, которая на 0,4 мм отличается от более точного значения, т.е. сходимость значений 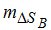 , определенных по формуле (3) и формуле (4), является удовлетворительной. Следовательно, более простую и компактную формулу (4) можно использовать для оценки точности определения влажной составляющей поправки  ΔS_B .

Для наклонных расстояний 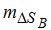 будет увеличиваться в (sec z_cp.) раз.

Формулу (1) целесообразно использовать при наличии высокоточного высотного профиля влажности и температуры. Если информация о распределении  е и Т  отсутствует, то наряду с использованием эмпирических формул   имеет смысл получить формулы для непосредственного определения влажной составляющей поправки в расстояние.

При рассмотрении этого вопроса воспользуемся идеей метода однородных атмосфер. Этот метод для светового диапазона электромагнитного излучения разработан и рассмотрен в работах [2,3].

При определении поправки  ΔS_в  методом однородных атмосфер атмосферу разбивают на участки (слои), в каждом из которых индекс преломления  N_в  является величиной постоянной, равной его значению на нижней границе слоя. При разбивке атмосферы или ее части на два слоя

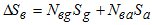 ,                                                 (5)

где  N_вg , N_ва – индексы преломления влажной составляющей в слоях  g  и  а ;   S_g , S_a – длина пути траектории ЭМВ в слоях  g  и  а  соответственно.

  Учитывая, что расстояние  S = S_g + S_a , a  S_a = S – S_g  , вместо (5) находим

 .

Примем 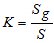  . С учетом этого

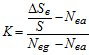.                                                          (6)

Для вертикального расстояния  S = H_a , а вместо (6) имеем

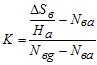.                                                           (7)

Принимая  К = 0,5 – q , после преобразований вместо (5) получим

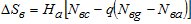 ,                                         (8)

где    .

В формуле (8) все аргументы, кроме  q , имеют отношение к начальной и конечной точкам траектории ЭМВ, поэтому необходимо найти зависимость  q  или связанную с этой величиной 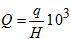   от значения  H .

Исследования показали, что величина  Q  хорошо аппроксимируется полиномом второй степени

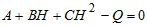 .                                               (9)

Коэффициенты уравнения (9), определенные по методу наименьших квадратов,

А = 19,017802  ,  В = 2,2432542  ,  С = -0,1490964  .

С учетом этих коэффициентов с сохранением шести значащих цифр вместо (9) имеем

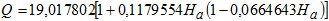 ,                     (10)

где  Н_а – в км.

Подставляя в формулу (8) вместо  q  его значение, находим

.  (11)

При  N_ва = 0  ,

 .

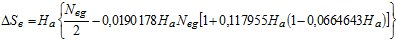Практически  N_ва = 0 можно считать при  Н_а = 11 км. С учетом этого обстоятельства

 .

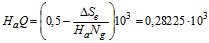С учетом полученного значения при  N_вa = 0,  для условий близких к принятым при выводе формул

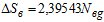 .                                                        (12)

Практически целесообразно считать  N_вa = 0  уже при  Н_а ≥ 10,6 км, т.е. при             Н_а ≥ 10,6 км  ΔS_в  в вертикальное расстояние нужно вычислять по формуле (12).

При других условиях коэффициент при  N_вg  в формуле (12) может отличаться от приведенного.

Исследования показали, что значение поправок  ΔS_в  за влажную составляющую в наклонные расстояния целесообразно так же, как за сухую составляющую, определять по формуле

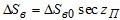 ,                                                            (13)

где  ΔS_в0 – поправка в вертикальные расстояния в пункте приема ЭМВ.

Выполненные исследования позволили для определения  z_П  получить эмпирическую формулу

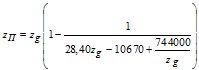 ,                                                   (14)

где зенитные расстояния  z_g  в пункте приема сигнала выражены в градусах дуги. Выполненное сравнение значений  ΔS_в , определенных по формулам (13), (14) и методом численного интегрирования, показало, что формулы (13), (14) являются довольно точными при условии высокоточного определения  ΔS_в0  в вертикальные расстояния, которые при известном высотном профиле упругости водяного пара и температуры целесообразно определять методом численного интегрирования.

Литература

1. Куштин В.И. Учет влияния атмосферы на результаты измерения длин радиоэлектронными системами. М., 2003, 171 с.

2. Куштин И.Ф. Учет рефракционных поправок в дальность методом однородных атмосфер // Тезисы для всесоюзного научно-практического совещания по проблемам совершенствования аппаратурных средств и таблиц для определения электромагнитных волн в земной атмосфере. – Иркутск, 1984, с. 71 – 73.

3. Куштин В.И. Точность определения поправок в дальность методом однородных атмосфер. – Геодезия и фотограмметрия. Ростов-на-Дону: РИСИ, 1988, с.34 – 44.