Расчетная модель радиального подшипника скольжения с повышенной несущей способностью, работающего на микрополярной смазке с учетом ее вязкостных характеристик от давления
Аннотация
Дата поступления статьи: 21.10.2013Как известно, в настоящее время в качестве модели гидродинаимческой смазки в подшипнике скольжения широко используется микрополярная смазка. Существенным недостатком существующих рабочих моделей подшипников скольжения, работающих на микрополярной смазке заключается в том, что здесь не учитывается зависимость вязкостных характеристик микрополярной смазки от давления. Естественно, возникает необходимость не только учета зависимости вязкостных характеристик от давления при разработке аналитического метода прогнозирования оптимальных по несущей способности характеристик, присущих микрополярным смазкам, но и прогнозирование оптимального профиля опорной поверхности радиального подшипника [1-3].
Решению данной задачи посвящена данная работа.Ключевые слова: радиальный подшипник, режим трения, проницаемость пористого слоя, микрополярная смазка.
Как известно, в настоящее время в качестве модели гидродинамической смазки в подшипнике скольжения широко используется микрополярная смазка. Существенным недостатком существующих рабочих моделей подшипников скольжения, работающих на микрополярной смазке заключается в том, что здесь не учитывается зависимость вязкостных характеристик микрополярной смазки от давления. Естественно, возникает необходимость не только учета зависимости вязкостных характеристик от давления при разработке аналитического метода прогнозирования оптимальных по несущей способности характеристик, присущих микрополярным смазкам, но и прогнозирование оптимального профиля опорной поверхности радиального подшипника. [1-3]
Решению данной задачи посвящена данная работа.
1. Постановка задачи
Как и в работе [4] рассмотрим установившееся движение микрополярной жидкости в зазоре радиального подшипника бесконечной длины. Предполагается, что подшипник неподвижен, а шип вращается вокруг своей неподвижной оси с угловой скоростью 
(рис. 1). Также предполагается,
. (1)
Здесь 
– характерная вязкость ньютоновской смазки; 
и 
– характерные вязкости микрополярной смазки; 
– гидродинамическое давление; 
– экспериментальная постоянная величина.
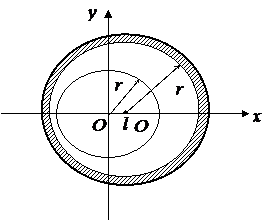
Рис. 1. Схематическое изображение шипа в подшипнике
Уравнение контуров шипа и подшипника запишем в полярной системе координат 
координат с полюсом в центре шипа:
, (2)
где 
– радиус шипа, 
– радиус кругового подшипника, 
– эксцентриситет; 
и 
малые величины одного порядка (
); 
– подлежит определению.
2 Основные уравнения и граничные условия
При разработке расчетной модели поставленной задачи в качестве основных уравнений берется система безразмерных уравнений движения микрополярной смазки для случая «тонкого слоя» с учетом (1), а также уравнение неразрывности
. (3)
Приведем связь размерных величин с безразмерными
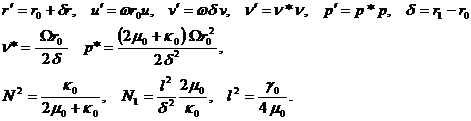(4)
Здесь 
– коэффициент вязкости для ньютоновской жидкости; 
– вектор скорости микровращения; 
– гидродинамическое давление в смазочном слое; 
– коэффициенты вязкости микрополярной жидкости;
– компоненты вектора скорости.
Безразмерная система уравнений (3) решается при следующих граничных условиях:
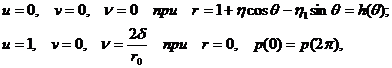(5)
где 
Решение системы уравнений (3)-(5) будем искать в виде рядов по степеням малого параметра 
.(6)
Подставим (6) в (3) и (5), тогда для нулевого приближения получим следующую систему уравнений и граничных условий к ним
(7) 
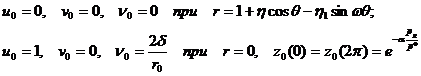. (8)
Найдем точное автомодельное решение системы уравнений (7)-(8):
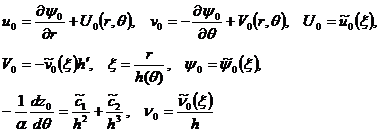(9)
Чтобы определить функций 
, 
, 
, 
, подставим (9) в (7) и (8), тогда с точностью до членов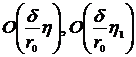 
получим следующую систему уравнений и граничных условий к ним:
(10)
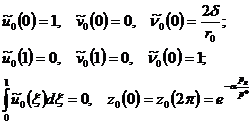. (11)
Проинтегрировав уравнения (10)-(11), в результате получим
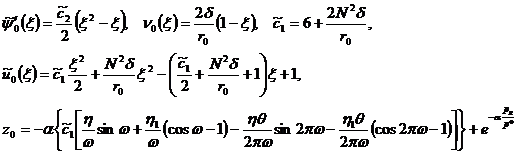. (12)
.
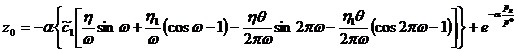Приведем сначала решение задачи для первого приближения. Учитывая (3) и (6), для первого приближения получим следующую систему уравнений и граничных условий к ним:
(13)
(14)
Решение системы уравнений (13)-(14) найдем непосредственным интегрированием. Используя разложение в ряд с точностью до членов 
, 
, получим
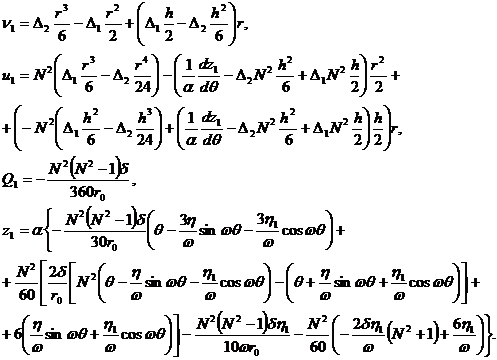(15)
С учетом выражения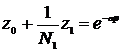 
для гидродинамического давления получим следующее выражение
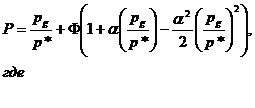
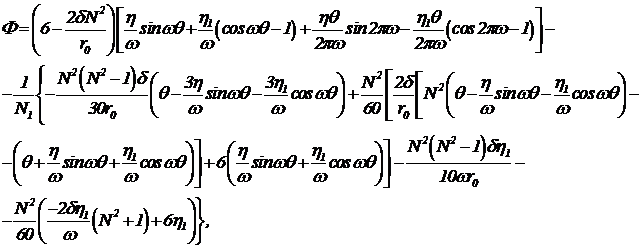
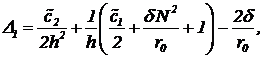
(16)
Используя найденное аналитическое выражение (16) для компонент поддерживающей силы получим следующие выражения:
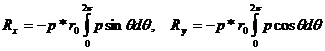(17)
Анализируя результаты численного решения, приведенные на рис. 2, показывают, что:
1. Характеристики микрополярной смазки и параметр 
[4] существенно влияют на несущую способность радиального подшипника.
2. С увеличением значений параметра 
несущая способность подшипника возрастает.
3. С увеличением значений параметра 
несущая способность подшипника убывает. При 
несущая способность подшипника стабилизируется.
4. При значении параметра 
близком к 0,5 рассматриваемый радиальный подшипник (по сравнению с 
) обладает свойством подшипника, так называемого, «двойного действия», по несущей способности.
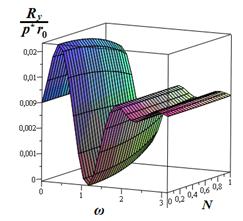
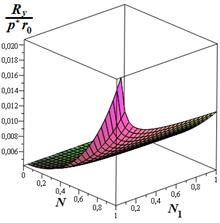
Рис. 2 Зависимости безразмерной несущей способности от параметров N, N1 и ω
Литература:
1. Ахвердиев К.С., Гидродинамический расчет радиального подшипника, работающего в нестационарном режиме на вязкопластичной смазке, обладающей микрополярными свойствами / М.А. Мукутадзе, А.Ю. Вовк, И.С. Семенко //. Вестник РГУПС. – 2008. - № 4. - С. 131–138.
2. Ахвердиев К.С, Математическая модель гидродинамической смазки радиального подшипника, работающего в нестационарном режиме на микрополярной смазке / М.А. Мукутадзе, М.А. Савенкова, А.Ю. Вовк // Вестник РГУПС. – 2008. - № 1. – С. 147–151.
3. Ахвердиев К.С., Гидродинамический расчет радиального подшипника скольжения, работающего в турбулентном режиме трения при неполном заполнении зазора вязкоупругой смазкой / М.А. Мукутадзе, В.А. Замшин, И.С. Семенко // Вестник машиностроения. – 2009. - № 7.- С. 11–17.
4. Вовк А.Ю., Прогнозирование значений безразмерных параметров микрополярных смазочных материалов с вязкоупругопластичными свойствами, обеспечивающих устойчивый режим работы подшипников скольжения / автореферат диссертация кандидата технических наук: 05.02.04; [Место защиты: Ростовский государственный университет путей и сообщения.] – Ростов-на-Дону. 2009. С. 167.
5. Конри, Об устойчивости пористых радиальных подшипников. Конструирование и технология машиностроения / Конри, Кузано // Вестник Машиностроения.- 1974. - № 2. - С. 206-216.
6. Ахвердиев, К.С., Об устойчивости двухслойных пористых радиальных подшипников / К.С. Ахвердиев, О.В. Муленко // Вестник РГУПС. - 2002. - № 3. – С. 5-7.
7. Кузано, Исследование коэффициента передачи упругой опоры качения в демпфере со сдавливаемой пленкой и пористой обоймой. / Кузано, Р.Е. Франк // Проблемы трения и смазки. - изд-во «Мир». – 1974. - № 1, - С. 54.
8. Gear C.W., Numarical Initial Value Problems in Ordinary Differential Equations / C.W. Gear. - Prentice-Hall, Inc., Englewood Cliffs. - N.J., 1972. – С. 52.
9. Мукутадзе М.А., Флек Б.М., Задорожная Н.С., Поляков Е.В., Мукутадзе А.М. Расчетная модель гидродинамической смазки неоднородного пористого подшипника конечной длины, работающего в устойчивом нестационарном режиме трения при наличии принудительной подачи смазки [Электронный ресурс] // «Инженерный вестник Дона», 2013 г., №3 – Режим доступа: http://ivdon.ru/magazine/archive/n3y2013/1765 (доступ свободный) – Загл. с экрана. – Яз. рус.
10. Дерлугян Ф.П., Щербаков И.Н. Обоснование процесса получения композиционных антифрикционных самосмазывающихся материалов с заданными техническими характеристиками методом химического наноконструирования. [Электронный ресурс] // «Инженерный вестник Дона», 2010 г., №4 – Режим доступа: http://ivdon.ru/magazine/archive/n4y2010/287 (доступ свободный) – Загл. с экрана. – Яз. рус.
11. Reynolds, O. On the theory of lubrication and its application to Mr. Beauchamp Tower”s experiments / O. Reynolds. – Phil. Trans. Roy. Soc. London, 1886, vol. 177, pt. 1.